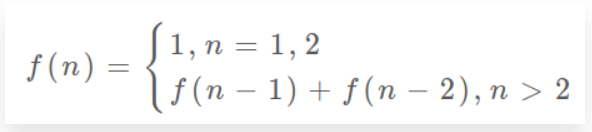本文详细介绍动态规划，包括

什么是动态规划?
能解决什么问题
动态规划的基本思想
适用条件
作用
算法框架以及优化
以及一道完整的动态规划题

什么是动态规划？

动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。(百度百科)

多阶段决策问题

在现实生活中，有一类活动的过程，由于它的特殊性，可将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。

因此各个阶段决策的选取不能任意确定，它依赖于当前面临的状态，又影响以后的发展。

当各个阶段决策确定后，就组成一个决策序列，因而也就确定了整个过程的一条活动路线。

这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程，这种问题称为多阶段决策问题。

在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化的过程为动态规划方法。

能解决什么问题？

动态规划算法通常用于求解具有某种最优性质的问题。

在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。

举例：凑硬币

给你 k 种面值的硬币，面值分别为 c1, c2 ... ck，每种硬币的数量无限，再给一个总金额 amount，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，算法返回 -1 。

例如：amount = 11，面值1，2，5

可能的解：

11

全部为1

10

1个2，9个1

…

3

2个5，1个1

上述例子存在多个可行解，也存在一个最优解(3)，动态规划就是求解这个最优解

基本思想

将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

通过保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。

用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。

适用条件

任何思想方法都有一定的局限性，动态规划也并不是万能的。

适用动态规划的问题必须满足最优化原理和无后效性

最优化原理（最优子结构性质）

一个最优化策略的子策略总是最优的。

举例：考全班第一名(假如只有语数英)

最优化策略：总分第一名

最优子策略

语文第一名

数学第一名

英语第一名

无后效应

对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。

每个状态都是过去历史的一个完整总结

作用

动态规划算法的目的：解决冗余

将某个问题划分成子问题的方法都可以用递归去实现

为什么有冗余?

子问题有重叠性

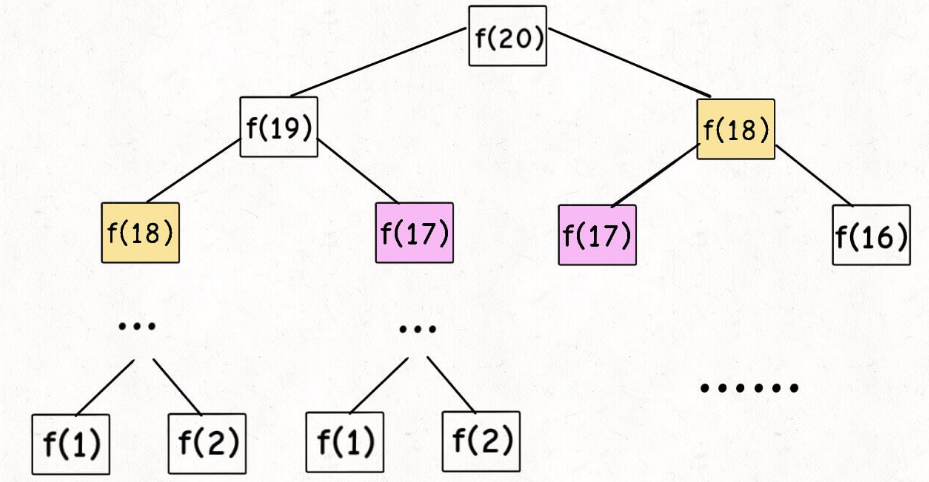
例如：计算斐波那契数列(斐波那契数列没有求最值，所以严格来说不是动态规划问题，只是为了弄明白什么是重叠子问题)

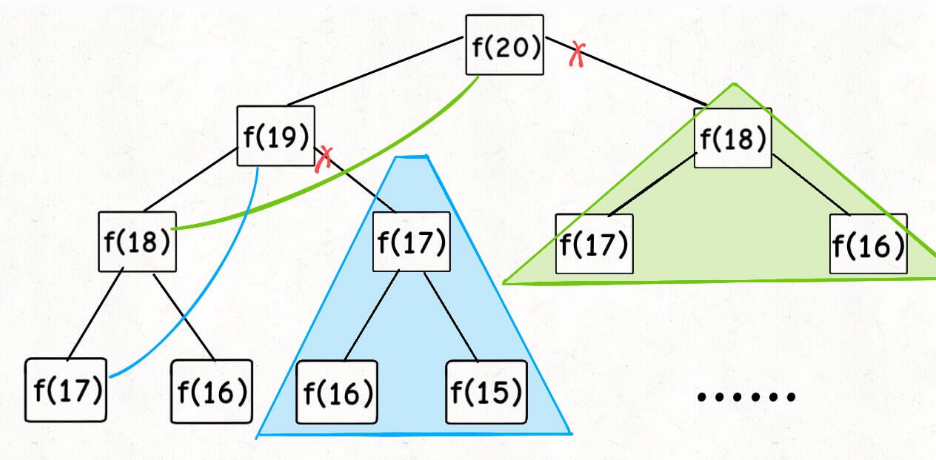
f(18)、f(17)、f(16)…都会被多次计算，我们希望同一个子问题只计算一次

解决冗余：把计算过的子问题存起来(db表)，当解决子问题时先去查表，若有答案则直接返回，没有则计算子问题

由此可以看出，dp是用空间换取时间(增加空间存储，减少了计算量)

// 不使用动态规划
var fib = function (n) {
    if(n == 1 || n == 2) return 1
    return fib(n-1) + fib(n-2)
}
// 从上图可以发现有很多子问题会被重复的计算

保存子问题答案

（自上而下解法）

var fib = function (n) {
    let memo = []
    return db(memo,n)
}
var db = function (memo,n){
    if(n == 0) return 0
    if(n == 1 || n == 2) return 1;
    if(memo[n] != undefined) return memo[n]
    memo[n] = db(memo,n-1) + db(memo,n-2)
    return memo[n]
}

memo表的作用：剪枝

后面是优化，本例子只是为了弄明白什么是重叠子问题，如果不想看优化可以跳到“算法框架”

（自下而上解法）

// 类似动态规划
// 声明了一个db数组(相当于一个表，保存已经得到解决的子问题的结果)
var fib = function (n) {
	if(n == 0) return 0;
    let db = []
    db[0] = 1;
    db[1] = 1;
    for(let i = 2;i<n;i++){
        db[i] = db[i-1] + db[i-2]
    }
    return db[n-1]
};

优化：节省空间（压缩状态表）

因为计算db(n)只需要db(n-1)和db(n-2)，前面的值都不需要了，所以不用保存，这里只需要用两个变量保存即可

var fib = function (n) {
	if(n == 0) return 0;
    if(n == 1 || n== 2) return 1
    let pre = 1,curr = 1;
    for(let i = 2;i<n;i++){
        let sum = pre + curr
        pre = curr
        curr = sum
    }
    return curr
};

算法框架

通过上面的学习，我们对动态规划有了一定的认识了。通过前人的大量实践和总结，得到了以下方法。

请确保已明白以下概念(上文都有涉及)

重叠的子问题

备忘录(或者DB table)

最优子结构

新增概念

base case

最小子问题：例如上面斐波那契数列的fib(0)、fib(1)和fib(2)

状态

和开头提到的多阶段决策的状态一样

一般在决策过程中发生变化的变量

在上面的斐波那契数列中就是n

状态转移方程

在当前状态做了某个选择后会转移到下一个状态

上面的斐波那契数列的转移方程是

把 fib(n) 想做一个状态 n，这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来

重叠子问题、最优子结构、状态转移方程就是动态规划三要素

写出状态转移方程是最困难的

为什么是以上三要素？

求解动态规划的核心问题是穷举所有可行解。

穷举所有可行解其实并不是一件容易的事，只有列出**正确的状态转移方程**，才能正确地穷举。

暴力穷举的话效率会极其低下，所以需要备忘录或者DP table来优化穷举过程，避免不必要的计算

态规划问题一定会具备最优子结构，才能通过子问题的最值得到原问题的最值

动态规划套路：确定状态->根据状态得到base case -> 确定状态转移方程 -> 定义 dp 数组/函数的含义

优化：压缩状态表

实践

问题

leetcode上322题：零钱兑换

问题描述

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

// 函数签名
var coinChange = function(coins, amount) {

};

示例

1
2
3

输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

1 2	输入：coins = [2], amount = 3 输出：-1

解决

解题思路

划分子问题

将amount进行划分，变成一个个子问题，即所有子问题状态：amount - coins[i] (i=0,1,2,…,coins.length-1)

1.确定状态

amount就表示状态
每次决策(选择一个硬币)后状态都会从 amount 变为 amount - coins[i]

2.确定base case

子问题状态的可能有三种
- 大于0、等于0、小于0
  - 大于0继续划分子问题
由划分子问题状态可以得到base case
- 等于0：可行解的一种，返回硬币数量
- 小于0：这种决策序列没有可行解，返回-1

3.状态转移方程

说明：min{dp(n-coin) + 1 | coin∈coins} , n>0

当n>0时，在状态n的时候，进行coins.length次的决策，取里面决策后的最小值
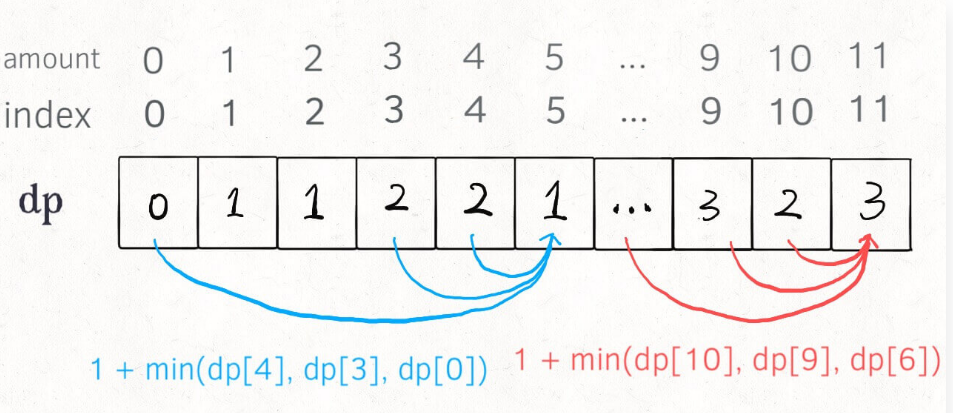
- 例如n=11，coins = [1,2,5]
  - min( db(10), db(9), db(6)) ，即得到最优子结构

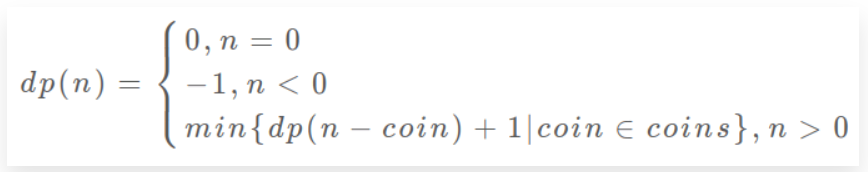
暴力解法(lc上显示超时)

var coinChange = function (coins, amount) {
    const db = (status) => {
        let res = Number.MAX_SAFE_INTEGER
        if (status == 0) return 0
        if (status < 0) return -1
        for (coin of coins) {
            let subProblem = db(status - coin)
            if (subProblem == -1) continue
            res = Math.min(res, subProblem + 1)
        }
        return res == Number.MAX_SAFE_INTEGER ? -1 : res
    }
    return db(amount)
};

备忘录解法

消除重复子问题

var coinChange = function (coins, amount) {
    let memo = new Map();
    const db = (status) => {
        if (status == 0) return 0
        if (status < 0) return -1
        if(memo.get(status)) return memo.get(status)
        let res = Number.MAX_SAFE_INTEGER

        for (coin of coins) {
            let subProblem = db(status - coin)
            
            if (subProblem == -1) continue
            res = Math.min(res, subProblem + 1)
        }
        memo.set(status,res == Number.MAX_SAFE_INTEGER?-1:res)
        return memo.get(status)
    }
    db(amount)
    return db(amount)
};

迭代解法(自底向上)

var coinChange = function (coins, amount) {
    // 数组大小为 amount + 1，初始值也为 amount + 1
    let dbTable = Array.from({length: amount+1}, () => amount+1)
    // base case
    dbTable[0] = 0
    // 遍历所有状态
    for(let status = 0;status < dbTable.length;status++){
        for(coin of coins){
            if(status - coin >=0) {
                dbTable[status] = Math.min(dbTable[status],1+dbTable[status - coin])
            }
        }
    }
    return (dbTable[amount] == amount + 1)?-1:dbTable[amount]
};

为啥 dp 数组初始化为 amount + 1 呢？

因为凑成 amount 金额的硬币数最多只可能等于 amount（全用 1 元面值的硬币），所以初始化为 amount + 1 就相当于初始化为正无穷，便于后续取最小值。

为啥不直接初始化为 int 型的最大值 Integer.MAX_VALUE 呢？

因为后面有 dp[i - coin] + 1，这就会导致整型溢出。

参考

百度百科

labuladong(图片也源自此)