遗传算法解决TSP问题

TSP问题

假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。

• 路径的选择目标是要求得的路径路程为所有路径之中的最小值。

即：

• 已给一个n个点的完全图，每条边都有一个长度，求总长度最短的经过每个顶点正好一次的封闭回路
  • 如果把所有路径进行组合，哪就是n^n^种

早期的研究者使用精确算法求解该问题，常用的方法包括：分枝定界法、线性规划法、动态规划法等。但是，随着问题规模的增大，精确算法将变得无能为力，因此，在后来的研究中，国内外学者重点使用近似算法或启发式算法，主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。

遗传算法

简介

遗传算法(GeneticAlgorithm ，GA )是通过模拟生物进化过程来完成优化搜索的

• 由美国J. Holland 教授提出的一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法

主要特点：

• 群体搜索策略和群体中个体之间的信息交换，搜索不以梯度信息为基础
• 适用于处理传统搜索方法难于解决的复杂和非线性问题，可广泛应用于组合优化、机器学习、自适应控制、规划设计和人工生命等领域
• 全局优化搜索算法
• 简单通用、鲁棒性强、适于并行处理以及应用范围广
  • 鲁棒是Robust的音译：稳健性或稳定性

遗传算法的结果

• 得到遍历过的所有结果的最优，但不一定是最优的结果
  • 如果把所有可能的情况都遍历了一遍，那就一定是最优的
  • 使用轮盘赌算法可以收敛得更快
    • 抽出来的都是距离比较小的路径，所以交换后路径更小的可能性比随机选的更大

核心思想

假设：

• 4个城市：1、2、3、4，最短路径的解是 [1,2,3,4]

概念	数据结构	类比
染色体	可行解	[1,2,3,4]、[2,1,4,3]、[3,2,4,1]
基因	可行解中的元素	1、2、3、4
染色体适应度(fitness value)	可行解的长度	[1,2,3,4]的总长度是5 [2,1,4,3]的总长度是10

遗传算法(GeneticAlgorithm ，GA )的核心：

• 不断的演变进化，挑选适应度更低的染色体，最后收敛
  • 演变进化：基因互换和变异

算法步骤

1.初始化N个染色体(染色体祖先部落)

• 计算适应度和适应度概率

2.通过基于互换和变异生成新的染色体，总数为N

3.将染色体祖先部落和新生成的染色体放在一起根据适应度进行排序,选出适应度较高的N个染色体形成下次迭代的染色体祖先部落

• 适应度高：总路径短

4.循环迭代以上步骤

迭代次数：(两种方式，根据业务场景具体选择)

• 限定迭代次数
• 限定允许范围
  • 事先设定一个可以接收的结果范围，当算法进行X次进化后，一旦发现了当前的结果已经在误差范围之内了，那么就终止算法

实现

注意：基因互换和变异可以有多种实现方式

基因交换(方式一)

• 从染色体祖先部落随机选取两个染色体(a,b)
• 在a中随机截取一段基于序列
• 在b中剔除与a截取出的相同的基于序列，同时将其他基因连接
• 将a截取的部分接入b尾部，即形成了新的染色体

基因交换(方式一)

• 轮盘赌算法选择两个染色体
• …
• 计算染色体适应度
• 计算染色体适应度概率
  • 选择基因交换时需要通过染色体适应度概率来选择，适应度较大的染色体选中概率较高
    • 这也就是为什么遗传算法能保留优良基因的原因
  • 染色体i被选择的概率 = 染色体i的适应度 / 所有染色体的适应度之和
• 交换仅仅是对原有的结果集进行选择，基因还是那么几个，只不过交换了他们的组合顺序。这只能保证经过N次进化后，计算结果更接近于局部最优解，而永远没办法达到全局最优解，所以需要引入变异

基于变异

• 从染色体祖先部落随机选取一个染色体
• 从中截取一段基因
• 打乱这一段基因后再插回形成了新的基因

适应度函数：从2N个染色体中选取N个适应度较高的染色体作为下次迭代的染色体祖先部落

• 复制：染色体祖先部落的染色体
• 替换：新的染色体

轮盘赌算法

目的：当根据适应度选择个体时，避免适应度低的被直接淘汰，即适应度低的还是有概率被选中的

参考

核心

1.个体选择概率

• 个体所占总体的比值

2.累积概率

• 各个个体的概率使用不同长度的线段来表示，这些线段组合成一条线段，线段的长度为1
• 个体的累计概率为其与其前面的概率之和
• 
• 某些个体明明选中概率很小但却因为它位置靠后而导致其累积概率很大而被选中的情况发生吗？
  • 不会上面例子跑1000遍的结果如下
• 

3.如何选择某个个体

实现步骤

（1）计算每个个体的被选中概率p(xi)

（2）计算每个部分的累积概率q(xi)

（3）随机生成一个数组m，数组中的元素取值范围在0和1之间，并将其按从小到大的方式进行排序。若累积概率q(xi)大于数组中的元素m[i]，则个体x(i)被选中，若小于m[i]，则比较下一个个体x(i+1)直至选出一个个体为止。

实现

文字描述

N个节点的完全图

1.初始化城市信息

graph = {
    "city1":(x1,y1),
    "city2":(x2,y2),
    # ...
	"cityN":(xn,yn),
}

• N是第N个城市

• x,y是经纬度

• 城市距离：直线距离(两点间距离)

2.随机生成N个祖先

• 初始化适应度：修改oldRoute[n].weight的值

# 祖先染色体
oldRoutes = [
	{
		route = ["city1","city3","city2",...,"cityN"],
		weight = w1,
	},
	{
		route = ["city2","city1","city3",...,"cityN"],
		weight = w2,
	},
	#...
]

3.交换：使用轮盘赌算法选取两个祖先染色体

• 进行基因交换

4.变异：使用轮盘赌算法选取一个祖先染色体

• 进行基因变异

注意：基因交换和变异的总数为N

5.选择

• 从新生成的染色体和祖先染色体中选择最优的N条染色体作为下一次迭代的祖先染色体

伪代码

# 用TTL控制循环
# 当最优与上一次最优相同时，TTL-1
# TTL为0时返回结果

def TSP(old,best,TTL):
    if(TTL==0):
        return best #看要输出什么就返回什么
    N = len(old)
    # sNum + vNum = N   
    sRoutes = routeSwitch(old,sNum)  # 基因交换得到sNum条染色体
    vRoutes = routeVariation(vNum)   # 基因变异得到vNum条染色体
    newParent = select(old,sRoutes,vRoutes,N) #从old,sRoutes,vRoutes选出N条最合适的染色体
    newBest = getBest(newParent) # 获取最优路线权值
    if(newBest == best):
        TTL = TTL -1
    return TSP(newParent,newBest,TTL)

因为最后只需要那个best结果，而不需要中间迭代的结果，所以可以不用递归

• 使用一个全局变量，用于保存最后的结果
• (递归可能会爆栈)

result = {}

def TSP(old,best,TTL):
    ancestor = old #深拷贝
    while not TTL == 0:
        # 进化
        sRoutes = routeSwitch(ancestor,sNum)  # 基因交换得到sNum条染色体
        vRoutes = routeVariation(ancestor,vNum)   # 基因变异得到vNum条染色体
        # 选择
        ancestor = selectBestRoutes(ancestor,sRoutes,vRoutes,N) #从old,sRoutes,vRoutes选出N条最合适的染色体
        # 判断
        newBest = getBest(ancestor) # 获取最优路线权值
        if(newBest == best):
            TTL = TTL -1
        else:
            TTL重置
    #迭代结束
    result = getBestRoute(old)

实验结果

代码说明

• TSP.py
  • 遗传算法、轮盘赌算法代码
• main.py
  • 执行遗传算法，修改初始化城市信息
• testTSP.py
  • 测试TSP.py中的函数

运行main.py

基因交换部分示例

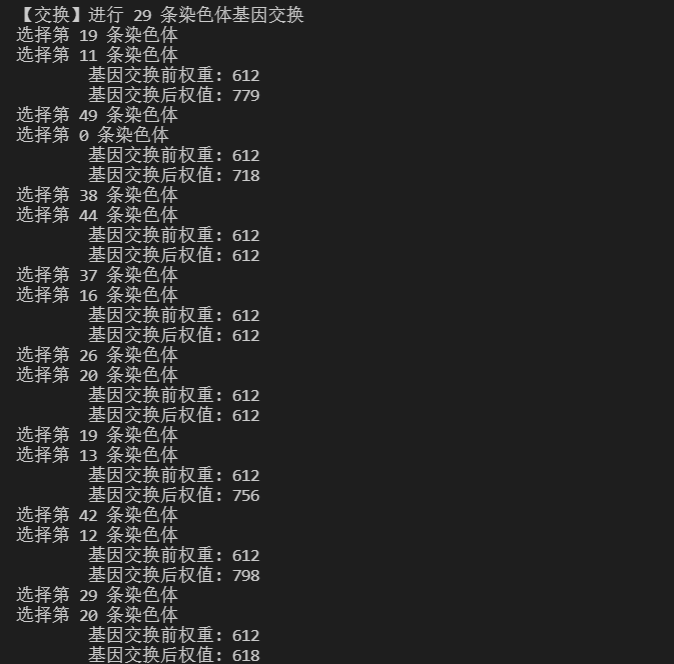
基因变异部分示例

实验结果